fullscreen
timer
qrcode
plickers
selector
edit
reset

Shading Intro

COS350 - Computer Graphics

Shading

without shading, we can perceive silhouettes, but nothing else

Shading
[ Vantablack by Surrey NanoSystems ]

Shading

we can approximate real world by simulating light bouncing around in scene of objects with modeled materials, lighting, participating media, vision systems, etc.

\[\begin{array}{rcl} L_o(\point{x}, \omega_o) & = & L_e(\point{x}, \omega_o) + L_r(\point{x}, \omega_o) \\ L_r(\point{x}, \omega_o) & = & \int_\Omega \rho(\point{x}, \omega_i, \omega_o) L_i(\point{x}, \omega_i) (\omega_i \cdot \direction{n}) d\omega_i \end{array}\]

[ Wikipedia: Rendering Equation ]

Shading

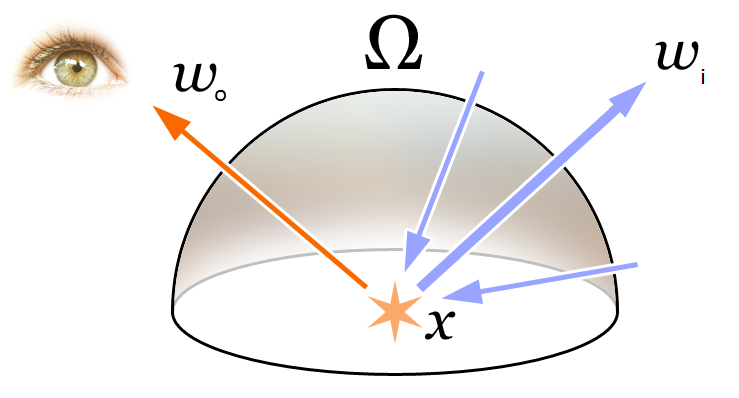
we can approximate real world by simulating light bouncing around in scene of objects with modeled materials, lighting, participating media, vision systems, etc.

\[\begin{array}{rcl} L_o(\point{x}, \omega_o) & = & L_e(\point{x}, \omega_o) + L_r(\point{x}, \omega_o) \\ L_r(\point{x}, \omega_o) & = & \int_\Omega \rho(\point{x}, \omega_i, \omega_o) L_i(\point{x}, \omega_i) (\omega_i \cdot \direction{n}) d\omega_i \end{array}\]

Note: the incoming light (\(L_i\) along \(\omega_i\)) can come:

Simplified rendering equation

we can approximate real world by simulating light bouncing around in scene of objects with modeled materials, lighting, participating media, vision systems, etc.

\[\begin{array}{rcl} L_o(\point{x}, \omega_o) & = & L_e(\point{x}, \omega_o) + L_r(\point{x}, \omega_o) \\ L_r(\point{x}, \omega_o) & = & \int_\Omega \rho(\point{x}, \omega_i, \omega_o) L_i(\point{x}, \omega_i) (\omega_i \cdot \direction{n}) d\omega_i \end{array}\]

we will simplify the rendering equation by ignoring \(L_e\), replace the integral with a sum, splitting reflectance into diffuse and specular, and handling indirect and reflection separately \[ c = \overbrace{\rho_d L_a}^{\text{indirect}} + \overbrace{\sum\nolimits_{i} \underbrace{(\rho_d + \rho_s)}_{\f_r} \* \underbrace{L_i \* V_i(\tilde\p)}_{L_i} \* \underbrace{| \hat\n \* \hat\l_i |}_{\omega_i \cdot \direction{n}}}^{\text{direct}} \, +\, \overbrace{k_r \ \mathrm{raytrace}(\tilde\p,\hat\r)}^{\text{reflection}} \]

shading intro

a moment for a word...

Gen 1:1–5 (ESV)

“

1 In the beginning, God created the heavens and the earth. 2 The earth was without form and void, and darkness was over the face of the deep. And the Spirit of God was hovering over the face of the waters.

3 And God said, "Let there be light,"" and there was light. 4 And God saw that the light was good. And God separated the light from the darkness. 5 God called the light Day, and the darkness he called Night. And there was evening and there was morning, the first day.

”

shading intro

lighting: sources of energy (illumination)

Lighting

Light Source Models

describe how light is emitted from light sources


two categories of lighting models


will use empirical models in this class

Ray Tracing Lighting Model

Point Lights  #
\(\point{p}\) : intersect loc
intersect.frame.o
\(\point{s}\) : light loc
light.frame.o
\(k_l\) : light intensity
light.kl

Directional Lights
\(\direction{d}\) : light direction
light.frame.z
\(k_l\) : light intensity
light.kl

Spot Lights
\(\point{p}\) : intersect loc
intersect.frame.o
\(\point{s}\) : light loc
light.frame.o
\(\frame{f}\) : light frame
light.frame
\(k_l\) : light intensity
light.kl

Spot Lights

Attenuation function can be arbitrary. For example,

[ Wikipedia: Gobo (lighting) ]

Incident Light / Cosine falloff  #
\(\direction{n}\) : intersect normal
intersect.frame.z
\(\direction{l}\) : light direction
(prev slides)

shading intro

materials: modeling how light interacts with surface

Real-World Materials

Metals Dielectric
[ Marschner 2004 ]

Real-World Materials

Metals Dielectric
[ Marschner 2004 ]

Surface Reflectance

Reflectance (Shading) Models

two categories of reflectance models


will use empirical models in this class

Reflectance Model

break reflectance model into two components:

Lambert Diffuse Model  #
left-to-right: increasing \(k_d\)
left-to-right: increasing \(k_d\)
\(k_d\) : diffuse reflection
intersection.material.kd

Image so far

now we can begin to understand the 3D shape of the objects, but they still look like the same material (only different color)

\[c = k_d \* L \* | \direction{n} \* \direction{l} | \]
\(k_d\) : diffuse reflection
intersection.material.kd
\(\direction{n}\) : intersect normal
intersection.frame.z
\(\direction{l}\), \(L\) : light direction, response
(light slides)

why are the balls are lit from below? (will take care of this soon)

Phong specular model  #
left-to-right: increasing \(n\); top-to-bottom: increasing \(k_s\)
left-to-right: increasing \(n\); top-to-bottom: increasing \(k_s\)
[ The Surprising Link Between the Vietnam War and 'Toy Story' | Time ]

Blinn-Phong specular model  #
\(k_s\) : specular reflection
intersection.material.ks
\(n\) : specular shininess
intersection.material.n
\(\direction{n}\) : intersect normal
intersection.frame.z
\(\direction{l}\) : light direction
(light slides)
\(\direction{v}\) : view direction
-ray.d

Image so far

objects appear distinct in terms of glossiness

\[c = \left( k_d + k_s \max(0,\hat\n \* \hat\h)^n \right) \* L \* | \direction{n} \* \direction{l} | \]

Reflectance Model with Multiple Lights  #

when there are multiple lights, add contribution of all lights for diffuse and specular

\[c = \sum\nolimits_{i} \left( \rho_d(\hat\l_i,\hat\v;\f) + \rho_s(\hat\l_i,\hat\v;\f) \right) \* L_i \* | \hat\n \* \hat\l_i | \]

for Lambert and Phong

\[c = \sum\nolimits_{i} \left( k_d + k_s \max(0,\hat\v \* \hat\r_i)^n \right) \* L_i \* | \hat\n \* \hat\l_i | \]

for Lambert and Blinn-Phong

\[c = \sum\nolimits_{i} \left( k_d+ k_s \max(0,\hat\n \* \hat\h_i)^n \right) \* L_i \* | \hat\n \* \hat\l_i | \]

Reflectance Model with Multiple Lights  #

Pseudocode for Lambert and Blinn-Phong

v_dir = -ray.dir      // view direction is opposite of ray direction
p = intersect.o       // intersection location
n_dir = intersect.n   // intersection normal

color = black
for each light {                              // assuming point light
    // compute lighting response
    s = light.o                               // light location
    l_dir = direction(s - p)                  // light direction
    l_dist = distance(s, p)                   // light distance
    L_res = light.kl / (distance * distance)  // light response
    cos_falloff = abs(dot(n_dir, l_dir))      // cosine falloff

    // compute material response
    h_dir = direction(v_dir + l_dir)
    brdf = mat.kd + mat.ks * max(0, pow(dot(n_dir, h_dir), mat.n)

    color += brdf * L_res * cos_falloff       // accumulate light
}

Image so far

the spatial relationships among the objects are difficult to discern

ex: how far above the plane are the two balls?

ex: why does light appear on top and bottom?

shading intro

illumination: patterns of light in the environment

Illumination Models

illumination models describe how light spreads in the environment

Ray Traced Shadows

no shadow shadow

Ray Traced Shadows

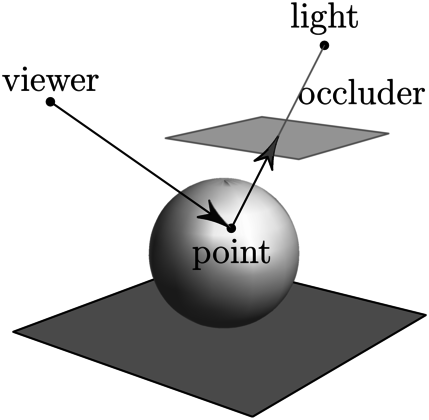
Ray Traced Shadows  #

\[c = \sum\nolimits_{i} (\rho_d + \rho_s) \* L_i \* V_i(\point{p}) \* | \direction{n} \* \direction{l}_i | \]
\(\point{p}\) : intersect loc, intersect.frame.o
\(\direction{l}\), \(\point{s}\) : light direction, location (light slides)

Image so far

it is now clear where the balls are in relation to the ground plane, but it is missing the light interaction between ground and balls

Ray Traced Shadows

implementation detail: numerical precision
\(t_{min} = 0\) \(t_{min} = \epsilon\)

Indirect illumination
[ PCG ]

Ambient Term Hack  #

for now, approx (poorly) diffuse reflections with a constant term

\[c = \rho_d L_a + \sum\nolimits_{i} (\rho_d + \rho_s) \* L_i \* V_i(\point{p}) \* | \direction{n} \* \direction{l}_i |\]
\(\rho_d\) : diffuse reflection
intersect.material.kd
\(\rho_s\) : specular reflection
intersect.material.ks, .n
\(L_a\) : ambient light
scene.ambient_light
\(L_i\), \(V_i\), \(\direction{l}\) : direct light
(light slides)
\(\point{p}\), \(\direction{n}\) : intersection
intersect.frame.o, .z

Important

the ambient term is outside the sum!

Ray Traced Reflections

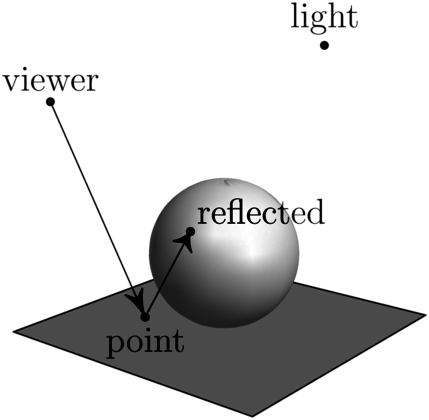
Ray Traced Reflections #

\[\begin{array}{rcl} c & = & \rho_d L_a + \left( \sum\nolimits_{i} (\rho_d + \rho_s) \* L_i \* V_i(\tilde\p) \* | \hat\n \* \hat\l_i |\, \right) + \\ & & \qquad+\, k_r \ \mathrm{irradiance}(\tilde\p,\hat\r) \end{array}\]

Image so far

ray traced refractions

\[\begin{array}{rcl} c & = & \rho_d L_a + \left( \sum\nolimits_{i} (\rho_d + \rho_s) \* L_i \* V_i(\tilde\p) \* | \hat\n \* \hat\l_i |\, \right) + \\ & & \qquad+\, k_r \ \mathrm{irradiance}(\tilde\p,\hat\r) + k_t \ \mathrm{irradiance}(\tilde\p,\hat\t) \end{array}\]

shading intro

Antialiasing

Antialiasing: removing jaggies

aliasing artifacts appear as jagged or saw-toothed due to under-sampling a curved shape

red object curves across image area
red object curves across image area
break image area into 3x3 pixels
break image area into 3x3 pixels
sample each pixel
sample each pixel
final 3x3 pixel image
final 3x3 pixel image
final 3x3 pixel image
final 3x3 pixel image
red object curves across image area
red object curves across image area
final 3x3 pixel image
final 3x3 pixel image
break image area into 9x9 subpixels
break image area into 9x9 subpixels
final 3x3 pixel image
final 3x3 pixel image
sample each subpixel
sample each subpixel
final 3x3 pixel image
final 3x3 pixel image
average subpixel samples into 3x3 pixels
average subpixel samples into 3x3 pixels
final 3x3 pixel image
final 3x3 pixel image
final antialiased 3x3 pixel image
final antialiased 3x3 pixel image

Antialiasing: removing jaggies

poor-man antialiasing:

Ray tracing pseudocode

original code with one sample per pixel

\[u = \frac{x + 0.5}{w} \qquad v = 1 - \frac{y + 0.5}{h} \]

for each pixel {
    determine viewing direction
    intersect ray with scene
    compute illumination
    store results in pixel
}

Anti-aliased Ray tracing pseudocode  #

updated code with multiple samples per pixel

\[u = \frac{x + (i + 0.5)/s}{w} \qquad v = 1 - \frac{y + (j + 0.5)/s}{h} \]

for each pixel {
    initialize color to black
    for each sample {  // note: numberOfSamples along x and along y
        determine viewing direction based on pixel and sub-pixel sample
        intersect ray with scene
        compute illumination
        accumulate result in color
    }
    store color / numberOfSamples^2 in pixel
}

Note: numberOfSamples (\(s\)) is per dimension, so the total number of samples per pixel is numberOfSamples squared (\(s^2\)), because images are two dimensional

image so far

low resolution, no antialiasing (\(1\) sample/pixel)
low resolution, no antialiasing (\(1\) sample/pixel)
low resolution, with antialiasing (\(3^2=9\) samples/pixel)
low resolution, with antialiasing (\(3^2=9\) samples/pixel)
full resolution, with antialiasing (\(3^2=9\) samples/pixel)
full resolution, with antialiasing (\(3^2=9\) samples/pixel)

shading intro

appendices

Appendix a: Snell's Law for refraction  #

Light travels slower through a medium than through a vacuum. We capture this slowness by the index of refraction equation \(n = \frac{c}{v}\), where \(c\) is speed of light in a vacuum and \(v\) is speed of light in the medium. Note: good approximations for a few media are:

\(n\) medium \(n\) medium
1.0 air 1.3 water
1.5 glass 2.4 diamond

Light follows a straight line when traveling in a single medium (ignoring general relativity). However, when light transitions from one medium to another with a different \(n\), the path bends at the interface. The amount of bend is modeled by Snell's Law:

\[ n_1 \sin \theta_1 = n_2 \sin \theta_2 \]

\[ \qquad \frac{\sin \theta_1}{\sin \theta_2} = \frac{n_2}{n_1} \qquad \]

[ original ]

Appendix a: Snell's Law for refraction

compute the direction of transmitted light using these equations:

\[\begin{array}{rcl} \eta & = & \frac{n_\textit{from}}{n_\textit{to}} \\ c_1 & = & \hat\n \cdot \hat\v \\ c_2 & = & \sqrt{1 - \eta^2 (1 - c_1^2)} \\ \hat\t & = & -\eta \hat\v - (\eta c_1 + c_2) \hat\n \end{array}\]
\(\hat\v\) viewing direction
\(\hat\n\) surface normal at point
\(\hat\t\) transmission direction
\(n\) index of refraction for medium

Note: total internal reflection if \(\eta^2 (1-c_1^2) \geq 1\) (expression under square root for \(c_2\) is negative!)

[ original ]

appendix b: fresnel  #

Transparent objects, such as glass or water, are both refractive and reflective. How much light they reflect vs the amount they transmit actually depends on the angle of incidence. The amount of transmitted light increases when the angle of incidence decreases.

We can compute the ratio of reflected (\(F_R\)) vs. refracted / transmitted (\(F_T\)) light using the Fresnel equations.

\[\begin{array}{rcl} F_{R\parallel} & = & \left(\frac{n_\textit{to} \cos \theta_1 - n_\textit{from} \cos \theta_2}{n_\textit{to} \cos\theta_1 + n_\textit{from}\cos\theta_2}\right)^2 \\ F_{R\bot} & = & \left(\frac{n_\textit{from}\cos\theta_2 - n_\textit{to}\cos\theta_1}{n_\textit{from}\cos\theta_2 + n_\textit{to}\cos\theta_1}\right)^2 \\ F_R & = & \frac{1}{2}\left( F_{R\parallel} + F_{R\bot} \right) \\ F_T & = & 1 - F_R \end{array}\]

[ original ]

appendix c: rendering equation  #

The central idea of this course is captured in one simple equation.


\[ L_o(\point{x}, \direction{\omega_o}) = L_e(\point{x}, \direction{\omega_o}) + \int_\Omega \rho(\point{x}, \direction{\omega_i}, \direction{\omega_o}) L_i(\point{x}, \direction{\omega_i}) (\direction{\omega_i} \cdot \direction{n}) d\omega_i \]


×